Por un error de precisión perdí una estatua
La precisión de la medida y la corrección de los errores de medición ocupan una parte importante en las técnicas de laboratorio de física. Para evitar estos errores se toman gran número de medidas y se calcula la media (suma de todas las medidas dividida por el número de ellas).
Para que comprendáis lo que puede suponer la precisión, contaré esta historia:
A un escultor le encargaron 13 estatuas de los personajes más importantes de la ciudad para que fueran colocados en las distintas plazas y parques del municipio. Cuando los terminó, los cargó en su furgoneta y fue a llevarlas al ayuntamiento. Por el camino un coche que se había saltado un semáforo le salió por un lado, tuvo que frenar bruscamente y desviar el volante.
Con este movimiento brusco sucedió lo que nadie quería, que las estatuas se rompieron dentro de la furgoneta, aunque no hubieron daños personales afortunadamente.
El trabajo de dos años del escultor había quedado destruido. Para solucionar este problema este escultor intentó arreglarlo pegando de nuevo los diversos trozos. Cuando terminó de pegarlos contó las figuras y sólo tenía 12 estatuas en lugar de 13, ¡y había utilizado todos los trozos!
Aquí tenéis las estatuas antes y después del accidente para que lo comprobéis. Si no te fías imprime esta hoja, recórtala por la parte móvil y comprueba tú mismo que no miento.
¡¡ Ha desaparecido una estatua.!!
Este es un problema típico de errores de precisión. ¿Se te ha ocurrido medirlos? ¿Cuándo son más altos?
Si una variación de altura te hace desaparecer una estatua, imagina los efectos a los que pueden dar lugar los errores o imprecisiones en las medidas.
Uno de los ejemplos más contundentes de lo dicho lo tenemos en la confirmación de una predicción de la Teoría de la Relatividad de Einstein, a la cual se pudo llegar gracias a una extraordinaria precisión en la medida para su época, que permitió detectar una ínfima desviación de la trayectoria de la luz al atravesar la órbita de Mercurio.
Por todo esto, no debemos ser despreciativos con los decimales, aunque nos gusten más los números enteros, pues según el campo que tomemos pueden suponer un enorme error.
Aunque esto ya parece que lo hemos aprendido un poco cuando apareció el euro y sus céntimos.
A un escultor le encargaron 13 estatuas de los personajes más importantes de la ciudad para que fueran colocados en las distintas plazas y parques del municipio. Cuando los terminó, los cargó en su furgoneta y fue a llevarlas al ayuntamiento. Por el camino un coche que se había saltado un semáforo le salió por un lado, tuvo que frenar bruscamente y desviar el volante.
Con este movimiento brusco sucedió lo que nadie quería, que las estatuas se rompieron dentro de la furgoneta, aunque no hubieron daños personales afortunadamente.
El trabajo de dos años del escultor había quedado destruido. Para solucionar este problema este escultor intentó arreglarlo pegando de nuevo los diversos trozos. Cuando terminó de pegarlos contó las figuras y sólo tenía 12 estatuas en lugar de 13, ¡y había utilizado todos los trozos!
Aquí tenéis las estatuas antes y después del accidente para que lo comprobéis. Si no te fías imprime esta hoja, recórtala por la parte móvil y comprueba tú mismo que no miento.
¡¡ Ha desaparecido una estatua.!!
Si una variación de altura te hace desaparecer una estatua, imagina los efectos a los que pueden dar lugar los errores o imprecisiones en las medidas.
Uno de los ejemplos más contundentes de lo dicho lo tenemos en la confirmación de una predicción de la Teoría de la Relatividad de Einstein, a la cual se pudo llegar gracias a una extraordinaria precisión en la medida para su época, que permitió detectar una ínfima desviación de la trayectoria de la luz al atravesar la órbita de Mercurio.
Por todo esto, no debemos ser despreciativos con los decimales, aunque nos gusten más los números enteros, pues según el campo que tomemos pueden suponer un enorme error.
Aunque esto ya parece que lo hemos aprendido un poco cuando apareció el euro y sus céntimos.
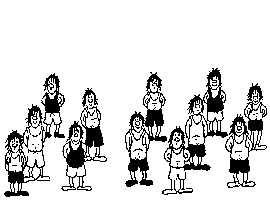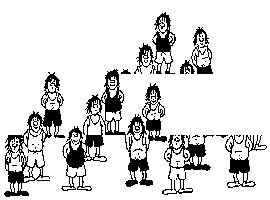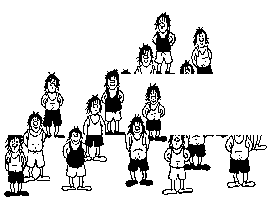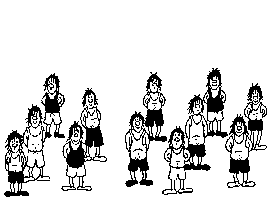
Comentarios
Publicar un comentario